

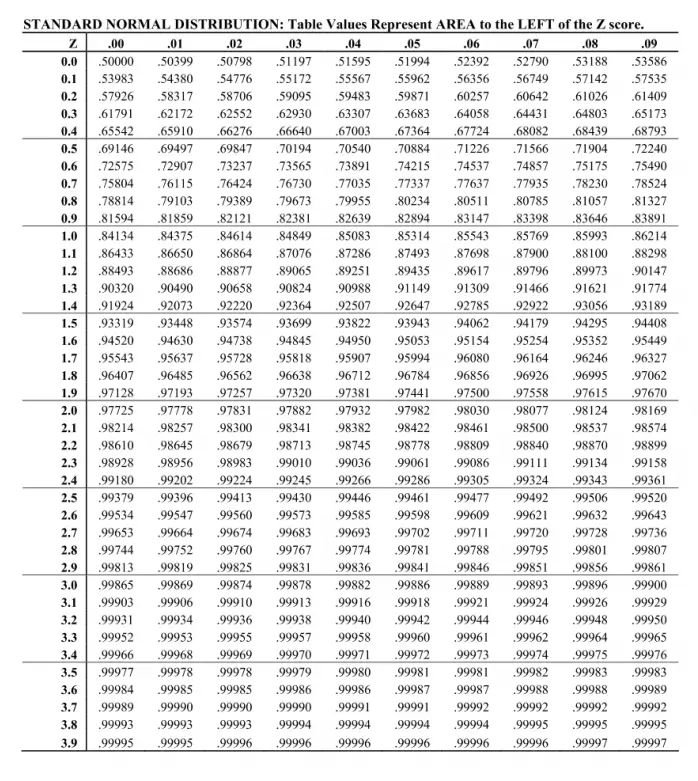
We all know that the P-value is the holy grail of introductory statistics. We will then use the test statistic to calculate a P-value and ultimately make a decision. The concept and interpretation of the z-score later becomes the concept and interpretation of the test statistic when we get to significance testing. If you have a well-written test, then everything that happens in class should be moving your students towards success on that test. You will know better which information to stress and you will choose your activities to help support your students’ learning and ability to be successful on the test. You must be familiar with your own test and the rubric used to grade it. But next year you will have this test written before teaching the unit. OK, so you might be in your first year and this is not humanly possible. But now technology exists ( applets, normalcdf) that can do this for us. Many stats teachers will claim that the reason we need students to calculate and understand z-scores is so that they can use a Table to find area under normal distributions. I often follow up with the question “Is this far from the mean?” Now every time in class that we calculate a z-score (and later a t-score), I call on that student to interpret: “Student, what is this z-score telling us?”

#STANDARD DEVIATION Z SCORE CALCULATOR FULL#
This is a full year commitment and is a paid position ($1 paid in full at the end of the year…but it is a great resume builder). Student: “Marty’s Chapter 1 test score is 1.8 standard deviations above the mean”īecause the z-score interpretation is so important, I hire a student to be in charge of this interpretation. What is a z-score of 1.8 telling us? And we arrive at the goal of the lesson: In pairs, have students discuss the meaning of the z-score. Next, we calculate the z-score for several students for the AP Stats test (mean = 70, SD = 10). When students share out their thoughts on this short activity, ask them to explain the (simple) mathematics they used to arrive at 3 and 2, and we get this:Īt this point, don’t worry at all about using Greek letter notation, as we are building a concept. But some students will start to realize that the AP Psych test is actually more impressive, as the score is 3 full standard deviations above the mean while the AP Stats score is only 2 standard deviations above the mean. Of course at first glance, the AP Stats test looks more impressive as 90 > 85. Mean = 70 SD = 10 Luke test score = 90ĪP Psych test. Which of Luke’s test scores is more impressive?ĪP Stats test. Luke scored a 90 on the AP Statistics test and an 85 on the AP Psychology test. The Chapter 1 AP Statistics test had an average of 70 and a standard deviation of 10 while the Chapter 1 AP Psychology test had an average of 70 and a standard deviation of 5. Students are given this scenario and asked to discuss in pairs: Rather than shoving the formula in front of students, try to put them in a situation where they discover the need for the concept of a z-score. But interpreting the z-score is a much more important concept for their future success. Most of our students will have no trouble calculating a z-score.


 0 kommentar(er)
0 kommentar(er)
